Completando la ilusión
Para que el juego sea completamente engañoso, no debemos limitarnos a los movimientos descritos anteriormente que son los que permiten volver a una situación en la que la suma de objetos de cada arista es trece. Antes o después de ejecutarlos, se pueden llevar a cabo otra serie de movimientos completamente inocuos, es decir, que no alteran en ningún caso la suma de la cantidad de objetos de cada arista. Algunos ejemplos de este tipo de movimientos serían los siguientes:
1. Trasladar o intercambiar objetos entre los dos grupos centrales de una misma arista.
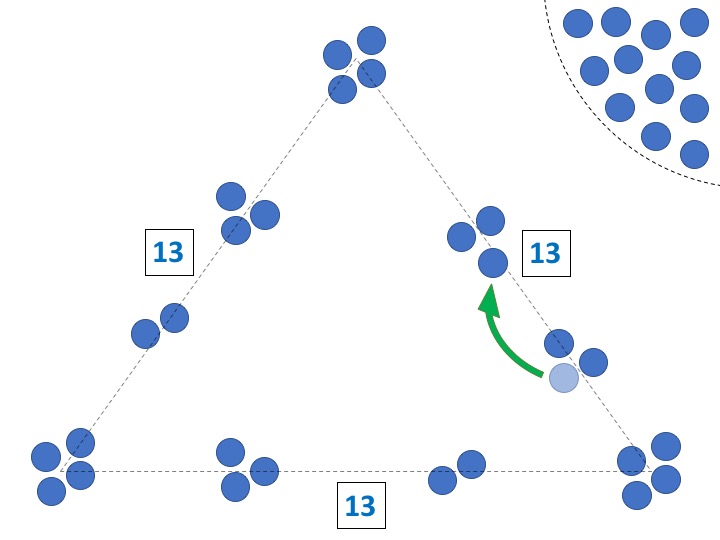
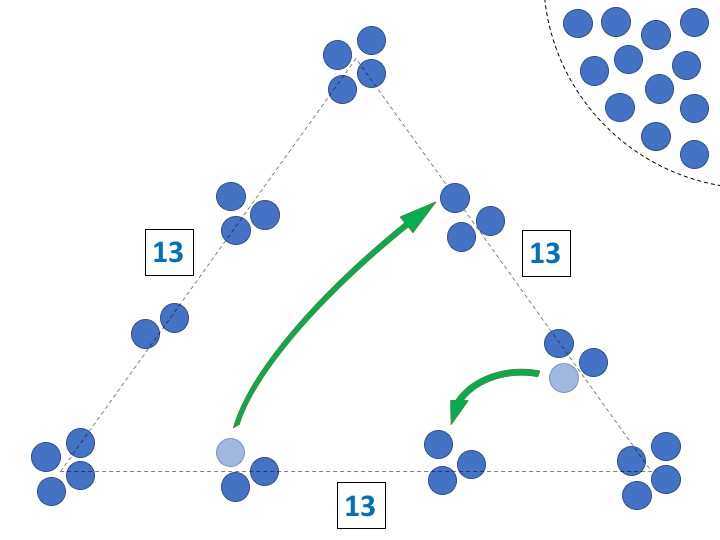
2. Intercambiar la misma cantidad de objetos entre los dos grupos centrales de diferentes aristas.
Si quieres saber más
El método utilizado en este juego se remonta al menos hasta el año 1633. En el libro Mathematical Recreations de Henry Van Etten (páginas 124-125) aparece el problema LXXII titulado Of the Game of square formes. El contexto es diferente, puesto que trata de soldados que tienen que defender las puertas y las esquinas de una plaza de manera que haya siempre 9 soldados en cada lado, planteándose el reto de cómo mantener ese número invariable si se incorporan más soldados.
Por otro lado, la disposición que hemos explicado para los grupos de objetos que forman el triángulo fue propuesta por Jim Steinmeyer en el juego Understanding the Bermuda Triangle publicado en su libro Impuzzibilities en 2002.
Como hemos comentado al principio, versiones anteriores de este juego utilizan una distribución de los grupos de objetos en forma de cuadrado o de rectángulo. Sin embargo, teniendo en cuenta que el efecto mágico que se quiere conseguir son las desapariciones de los objetos, el uso de una charla relacionada con el triángulo de las Bermudas y la posibilidad de distribuir los elementos utilizados siguiendo esa misma forma geométrica logran que el conjunto tenga una excelente coherencia estructural y narrativa.
También se encuentran entre mis favoritos los siguientes juegos basados en el mismo sistema:
- Perfect Ten Paper Clip Paradox, publicado por Paul Harris en su libro Secrets of the Astonishing Executive en 1991. Se utilizan clips de papel dispuestos en forma de cuadrado, de tal manera que los cuatro grupos de clips que forman cada lado suman un total de diez. En el interior del cuadrado se colocan varios clips adicionales que se van añadiendo de uno en uno a alguno de los grupos que forman el cuadrado. Tras cambiar la posición de determinados clips se comprueba que todos los lados siguen sumando diez.
- The pennies, vídeo publicado por Giovanni Livera en el que realiza un efecto similar utilizando en esta ocasión monedas distribuidas también en forma de cuadrado con diez monedas en cada arista.
- The Bermuda Runes, publicado por Peter Marucci en el que utiliza también la configuración del triángulo y usa pequeñas piedras con inscripciones rúnicas.
Por supuesto, este juego se podría realizar al revés, es decir, sacando objetos del triángulo o cuadrado que utilizamos en la configuración de partida y realizando a continuación los movimientos que permiten que la cantidad de objetos de cada lado sea la misma. Por ejemplo, si utilizas monedas, estás podrían representar lingotes de oro custodiados en una cámara acorazada y dar pie a otro tipo de charla en la que explicas que eres capaz de escamotearlos de uno en uno sin que nadie lo advierta y a pesar de que se hace recuento con frecuencia para que no se pierda ningún lingote. Una forma de presentarlo consistiría en hablar acerca de Fort Knox o del Banco de España y explicar como aprovechas tu conocimiento de los turnos de los vigilantes para llevarte un lingote durante el relevo. Después, muestras como los nuevos vigilantes vuelven a contar la cantidad de lingotes que hay en cada lado de la cámara acorazada, lo que provocará la sorpresa de los espectadores al ver que siguen sumando la misma cantidad que había inicialmente. En apariencia nada habría cambiado y los vigilantes continuarían su ronda con normalidad. Esto lo puedes repetir en varias ocasiones y finalizar explicando que fue así como te hiciste millonario ;-). Personalmente, cuando presento esta versión del juego utilizo una charla relacionada con la serie La casa de papel, porque la temática se presta perfectamente a ello, además de resultar muy familiar para la mayoría del público.


Había visto algún vídeo del juego , pero no entendía bien como funcionaba. Muchas gracias por la descripción tan detallada. Es muy curioso.
muy buena la matemática i yo ke soy un ñiño es toy en una escuela de la gapon en república dominicana
Fabuloso, genial, increíble, me gustaría saber más… muy buenas tus clases…Gracias…
Muchas gracias por tus palabras, Eduardo. Me alegro de que te haya parecido interesante.