Principio de la distribución oculta

Más tarde, autores como Edmé-Gilles Guyot en el segundo volumen de su obra Nouvelles récréations physiques et mathématiques  de 1769 y William Hooper en la edición de 1774 del libro Rational Recreations, describen como una superficie rectangular formada por 30 recuadros (10 x 3) se puede dividir en 4 trozos que una vez redistribuidos forman 2 rectángulos, uno compuesto por 20 recuadros (5 x 4) y otro por 12 (6 x 2). En este caso la suma de los 2 rectángulos da como resultado una superficie formada por 32 recuadros, es decir, 2 más que la superficie original.

Como curiosidad en la primera edición del libro de Guyot se publicó un dibujo erróneo: en lugar de mostrarse un rectángulo de superficie 6 x 2 apareció uno de superficie 6 x 3. William Hooper que plagió parcialmente el trabajo de Guyot, incluyo el mismo dibujo erróneo en el libro que publicó 5 años después y no lo corregiría hasta la publicación de la edición de 1782.

Enunciado del principio

El enunciado lo vamos a hacer a partir de una paradoja muy básica conocida como la paradoja de las líneas, que sería la versión más simplificada posible de este tipo de rompecabezas.

Si tenemos 10 líneas verticales de igual longitud ubicadas dentro de un rectángulo y trazamos una diagonal desde el vértice inferior izquierdo al vértice superior derecho, de manera que pase por el extremo inferior de la primera línea y el superior de la décima, podemos observar que la longitud de los segmentos que quedan por encima de la diagonal decrece en la misma proporción que crece la longitud de los segmentos que están por debajo.

Si cortamos el rectángulo por la diagonal se generarán dos triángulos rectángulos. Al deslizar el triángulo superior hacia la derecha y hacia arriba siguiendo la diagonal hasta que las líneas verticales coincidan, se observa que ahora solo hay 9 líneas verticales.

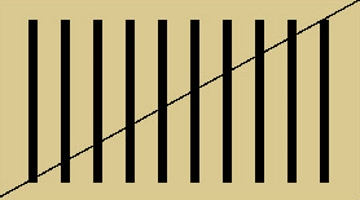
Situación inicial: 10 líneas

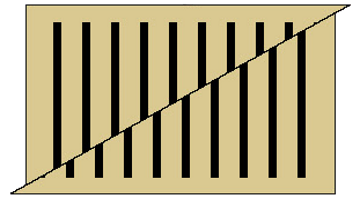
Corte diagonal y desplazamiento del triángulo superior hacia la derecha

Situación final: 9 líneas